Introduction

Imagine a dataset that records how individuals move through a city. The figure below shows what a datapoint from this set might look like. It depicts an individual, who we’ll call Bob, moving along a street and then stopping at a restaurant. This restaurant is one of two nearby branches of a chain of Donut Stores. Two other nearby restaurants are also shown on the map.

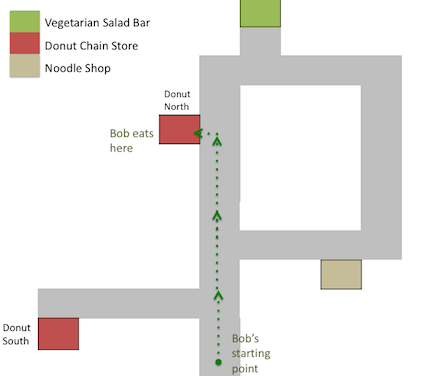
Given Bob’s movements alone, what can we infer about his preferences and beliefs? Since Bob spent a long time at the Donut Store, we infer that he bought something there. Since Bob could easily have walked to one of the other nearby eateries, we infer that Bob prefers donuts to noodles or salad.

Assuming Bob likes donuts, why didn’t he choose the store closer to his starting point (“Donut South”)? The cause might be Bob’s beliefs and knowledge rather than his preferences. Perhaps Bob doesn’t know about “Donut South” because it just opened. Or perhaps Bob knows about Donut South but chose Donut North because it is open later.

A different explanation is that Bob intended to go to the healthier “Vegetarian Salad Bar”. However, the most efficient route to the Salad Bar takes him directly past Donut North, and once outside, he found donuts more tempting than salad.

We have described a variety of inferences about Bob which would explain his behavior. This tutorial develops models for inference that represent these different explanations and allow us to compute which explanations are most plausible. These models can also simulate an agent’s behavior in novel scenarios: for example, predicting Bob’s behavior if he looked for food in a different part of the city.

Agents as programs

Making rational plans

Formal models of rational agents play an important role in economics refp:rubinstein2012lecture and in the cognitive sciences refp:chater2003rational as models of human or animal behavior. Core components of such models are expected-utility maximization, Bayesian inference, and game-theoretic equilibria. These ideas are also applied in engineering and in artificial intelligence refp:russell1995modern in order to compute optimal solutions to problems and to construct artificial systems that learn and reason optimally.

This tutorial implements utility-maximizing Bayesian agents as functional probabilistic programs. These programs provide a concise, intuitive translation of the mathematical specification of rational agents as code. The implemented agents explicitly simulate their own future choices via recursion. They update beliefs by exact or approximate Bayesian inference. They reason about other agents by simulating them (which includes simulating the simulations of others).

The first section of the tutorial implements agent models for sequential decision problems in stochastic environments. We introduce a program that solves finite-horizon MDPs, then extend it to POMDPs. These agents behave optimally, making rational plans given their knowledge of the world. Human behavior, by contrast, is often sub-optimal, whether due to irrational behavior or constrained resources. The programs we use to implement optimal agents can, with slight modification, implement agents with biases (e.g. time inconsistency) and with resource bounds (e.g. bounded look-ahead and Monte Carlo sampling).

Learning preferences from behavior

The example of Bob was not primarily about simulating a rational agent, but rather about the problem of learning (or inferring) an agent’s preferences and beliefs from their choices. This problem is important to both economics and psychology. Predicting preferences from past choices is also a major area of applied machine learning; for example, consider the recommendation systems used by Netflix and Facebook.

One approach to this problem is to assume the agent is a rational utility-maximizer, to assume the environment is an MDP or POMDP, and to infer the utilities and beliefs and predict the observed behavior. This approach is called “structural estimation” in economics refp:aguirregabiria2010dynamic, “inverse planning” in cognitive science refp:ullman2009help, and “inverse reinforcement learning” (IRL) in machine learning and AI refp:ng2000algorithms. It has been applied to inferring the perceived rewards of education from observed work and education choices, preferences for health outcomes from smoking behavior, and the preferences of a nomadic group over areas of land (see cites in reft:evans2015learning).

Section IV shows how to infer the preferences and beliefs of the agents modeled in earlier chapters. Since the agents are implemented as programs, we can apply probabilistic programming techniques to perform this sort of inference with little additional code. We will make use of both exact Bayesian inference and sampling-based approximations (MCMC and particle filters).

Taster: probabilistic programming

Our models of agents, and the corresponding inferences about agents, all run in “code boxes” in the browser, accompanied by animated visualizations of agent behavior. The language of the tutorial is WebPPL, an easy-to-learn probabilistic programming language based on Javascript refp:dippl. As a taster, here are two simple code snippets in WebPPL:

// Using the stochastic function `flip` we build a function that
// returns 'H' and 'T' with equal probability:

var coin = function() {
  return flip(.5) ? 'H' : 'T';
};

var flips = [coin(), coin(), coin()];

print('Some coin flips:');
print(flips);

// We now use `flip` to define a sampler for the geometric distribution:

var geometric = function(p) {
  return flip(p) ? 1 + geometric(p) : 1
};

var boundedGeometric = Infer({ 
  model() { return geometric(0.5); },
  method: 'enumerate',  
  maxExecutions: 20 
});

print('Histogram of (bounded) Geometric distribution');
viz(boundedGeometric);

In the next chapter, we will introduce WebPPL in more detail.