Modeling Agents with Probabilistic Programs
by Owain Evans, Andreas Stuhlmüller, John Salvatier, and Daniel Filan

Cognitive biases and bounded rationality

Optimality and modeling human actions

We’ve mentioned two uses for models of sequential decision making:

Use (1): Solve practical decision problems (preferably with a fast algorithm that performs optimally)

Use (2): Learn the preferences and beliefs of humans (e.g. to predict future behavior or to provide recommendations/advice)

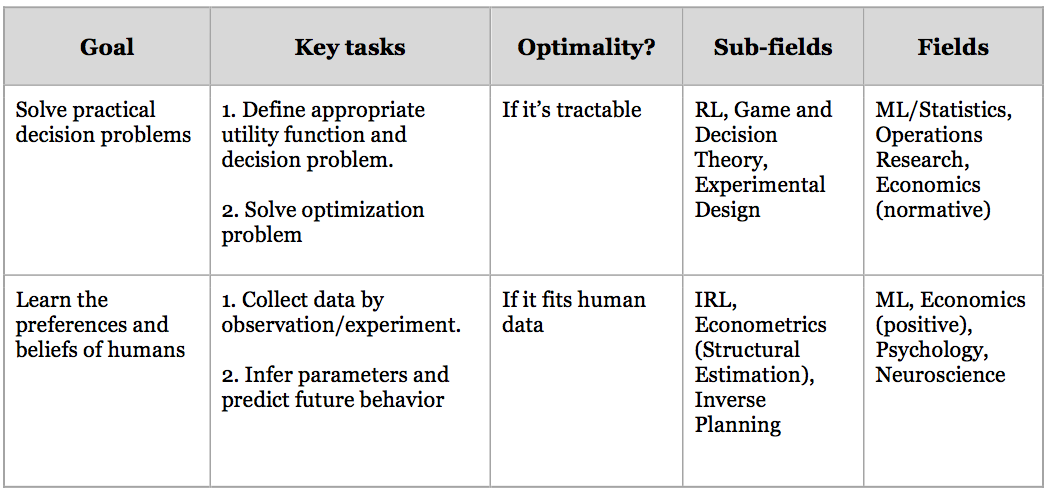
The table below provides more detail about these two uses1. The first chapters of the book focused on Use (1) and described agent models for solving MDPs and POMDPs optimally. Chapter IV (“Reasoning about Agents”), by contrast, was on Use (2), employing agent models as generative models of human behavior which are inverted to learn human preferences.

The present chapter discusses the limitations of using optimal agent modes as generative models for Use (2). We argue that developing models of biased or bounded decision making can address these limitations.

table

Table 1: Two uses for formal models of sequential decision making. The heading “Optimality” means “Are optimal models of decision making used?”.

Random vs. Systematic Errors

The agent models presented in previous chapters are models of optimal performance on (PO)MDPs. So if humans deviate from optimality on some (PO)MDP then these models won’t predict human behavior well. It’s important to recognize the flexibility of the optimal models. The agent can have any utility function and any initial belief distribution. We saw in the previous chapters that apparently irrational behavior can sometimes be explained in terms of inaccurate prior beliefs.

Yet certain kinds of human behavior resist explanation in terms of false beliefs or unusual preferences. Consider the following:

The Smoker
Fred smokes cigarettes every day. He has tried to quit multiple times and still wants to quit. He is fully informed about the health effects of smoking and has learned from experience about the cravings that accompany attempts to quit.

It’s hard to explain such persistent smoking in terms of inaccurate beliefs2.

A common way of modeling with deviations from optimal behavior is to use softmax noise refp:kim2014inverse and refp:zheng2014robust. Yet the softmax model has limited expressiveness. It’s a model of random deviations from optimal behavior. Models of random error might be a good fit for certain motor or perceptual tasks (e.g. throwing a ball or locating the source of a distant sound). But the smoking example suggests that humans deviate from optimality systematically. That is, when not behaving optimally, humans actions remain predictable and big deviations from optimality in one domain do not imply highly random behavior in all domains.

Here are some examples of systematic deviations from optimal action:

Systematic deviations from optimal action

These examples suggest that human behavior in everyday decision problems will not be easily captured by assuming softmax optimality. In the next sections, we divide these systematics deviations from optimality into cognitive biases and cognitive bounds. After explaining each category, we discuss their relevance to learning the preferences of agents.

Human deviations from optimal action: Cognitive Bounds

Humans perform sub-optimally on some MDPs and POMDPs due to basic computational constraints. Such constraints have been investigated in work on bounded rationality and bounded optimality refp:gershman2015computational. A simple example was mentioned above: people cannot quickly memorize random strings (even if the stakes are high). Similarly, consider the real-life version of our Restaurant Choice example. If you walk around a big city for the first time, you will forget the location of most of the restaurants you see on the way. If you try a few days later to find a restaurant, you are likely to take an inefficient route. This contrasts with the optimal POMDP-solving agent who never forgets anything.

Limitations in memory are hardly unique to humans. For any autonomous robot, there is some number of random bits that it cannot quickly place in permanent storage. In addition to constraints on memory, humans and machines have constraints on time. The simplest POMDPs, such as Bandit problems, are intractable: the time needed to solve them will grow exponentially (or worse) in the problem size refp:cassandra1994acting, refp:madani1999undecidability. The issue is that optimal planning requires taking into account all possible sequences of actions and states. These explode in number as the number of states, actions, and possible sequences of observations grows5.

So for any agent with limited time there will be POMDPs that they cannot solve exactly. It’s plausible that humans often encounter POMDPs of this kind. For example, in lab experiments humans make systematic errors in small POMDPs that are easy to solve with computers refp:zhang2013forgetful and refp:doshi2011comparison. Real-world tasks with the structure of POMDPs, such as choosing how to invest resources or deciding on a sequence of scientific experiments, are much more complex and so presumably can’t be solved by humans exactly.

Human deviations from optimal action: Cognitive Biases

Cognitive bounds of time and space (for memory) mean that any realistic agent will perform sub-optimally on some problems. By contrast, the term “cognitive biases” is usually applied to errors that are idiosyncratic to humans and would not arise in AI systems6. There is a large literature on cognitive biases in psychology and behavioral economics refp:kahneman2011thinking, refp:kahneman1984choices. One relevant example is the cluster of biases summarized by Prospect Theory refp:kahneman1979prospect. In one-shot choices between “lotteries”, people are subject to framing effects (e.g. Loss Aversion) and to erroneous computation of expected utility7. Another important bias is time inconsistency. This bias has been used to explain addiction, procrastination, impulsive behavior and the use of pre-commitment devices. The next chapter describes and implements time-inconsistent agents.

Learning preferences from bounded and biased agents

We’ve asserted that humans have cognitive biases and bounds. These lead to systemtic deviations from optimal performance on (PO)MDP decision problems. As a result, the softmax-optimal agent models from previous chapters will not always be good generative models for human behavior. To learn human beliefs and preferences when such deviations from optimality are present, we extend and elaborate our (PO)MDP agent models to capture these deviations. The next chapter implements time-inconsistent agents via hyperbolic discounting. The subsequent chapter implements “greedy” or “myopic” planning, which is a general strategy for reducing time- and space-complexity. In the final chapter of this section, we show (a) that assuming humans are optimal can lead to mistaken inferences in some decision problems, and (b) that our extended generative models can avoid these mistakes.

Next chapter: Time inconsistency I


Footnotes

  1. Note that there are important interactions between Use (1) and Use (2). A challenge with Use (1) is that it’s often hard to write down an appropriate utility function to optimize. The ideal utility function is one that reflects actual human preferences. So by solving (2) we can solve one of the “key tasks” in (1). This is exactly the approach taken in various applications of IRL. See work on Apprenticeship Learning refp:abbeel2004apprenticeship. ↩

  2. One could argue that Fred has a temporary belief that smoking is high utility which causes him to smoke. This belief subsides after smoking a cigarette and is replaced with regret. To explain this in terms of a POMDP agent, there has to be an observation that triggers the belief-change via Bayesian updating. But what is this observation? Fred has cravings, but these cravings alter Fred’s desires or wants, rather than being observational evidence about the empirical world. ↩

  3. With effort people can memorize these strings and keep them in memory for long periods. The claim is that if people do not make an attempt to memorize a random string, they will systematically forget the string within a short duration. This can’t be easily explained on a POMDP model, where the agent has perfect memory. ↩

  4. People learn the algorithm for long division but still make mistakes – even when stakes are relatively high (e.g. important school exams). While humans vary in their math skill, all humans have severe limitations (compared to computers) at doing arithmetic. See refp:dehaene2011number for various robust, systematic limitations in human numerical cognition. ↩

  5. Dynamic programming helps but does not tame the beast. There are many POMDPs that are small enough to be easily described (i.e. they don’t have a very long problem description) but which we can’t solve optimally in practice. ↩

  6. We do not presuppose a well substantiated scientific distinction between cognitive bounds and biases. Many have argued that biases result from heuristics and that the heuristics are a fine-tuned shortcut for dealing with cognitive bounds. For our purposes, the main distinction is between intractable decision problems (such that any agent will fail on large enough instances of the problem) and decision problems that appear trivial for simple computational systems but hard for some proportion of humans. For example, time-inconsistent behavior appears easy to avoid for computational systems but hard to avoid for humans. ↩

  7. The problems descriptions are extremely simple. So this doesn’t look like an issue of bounds on time or memory forcing people to use a heuristic approach. ↩