Time inconsistency II

Formal Model and Implementation of Hyperbolic Discounting

Formal Model of Naive and Sophisticated Hyperbolic Discounters

To formalize Naive and Sophisticated hyperbolic discounting, we make a small modificiation to the MDP agent model. The key idea is to add a variable for measuring time, the delay, which is distinct from the objective time-index (called timeLeft in our implementation). The objective time-index is crucial to planning for finite-horizon MDPs because it determines how far the agent can travel or explore before time is up. By contrast, the delays are subjective. They are used by the agent in evaluating possible future rewards but they are not an independent feature of the decision problem.

We use delays because discounting agents have preferences over when they receive rewards. When evaluating future prospects, they need to keep track of how far ahead in time that reward occurs. Naive and Sophisticated agents evaluate future rewards in the same way. They differ in how they simulate their future actions.

The Naive agent at objective time $t$ assumes his future self at objective time $t+c$ (where $c>0$ ) shares his time preference. So he simulates the $(t+c)$ -agent as evaluating a reward at time $t+c$ with delay $=c$ rather than the true delay $=0$ . The Sophisticated agent correctly models his $(t+c)$ -agent future self as evaluating an immediate reward with delay $=0$ .

To be more concrete, suppose both Naive and Sophisticated have a discount function $1/(1+kd)$ , where $d$ is how much the reward is delayed. When simulating his future self at $t+c$ , the Naive agent assumes he’ll discount immediate gains at rate $1/(1+kc)$ and the Sophisticated agent (correctly) assumes a rate of $1/(1+0)$ .

Adding delays to our model is straightforward. In defining the MDP agent, we presented Bellman-style recursions for the expected utility of state-action pairs. Discounting agents evaluate states and actions differently depending on their delay from the present. So we now define expected utilities of state-action-delay triples:

$EU[s,a,d] = \delta(d)U(s, a) + \mathbb{E}_{s', a'}(EU[s', a',d+1])$

where:

$\delta \colon \mathbb{N} \to \mathbb{R}$ is the discount function from the delay to the discount factor. In our examples we have (where $k>0$ is the discount constant):

$\delta(d) = \frac{1}{1+kd}$

$s' \sim T(s,a)$ exactly as in the non-discounting case.
$a' \sim C(s'; d_P)$ where $d_P=0$ for Sophisticated and $d_P=d+1$ for Naive.

The function $C \colon S \times \mathbb{N} \to A$ is again the act function. For $C(s'; d+1)$ we take a softmax over the expected value of each action $a$ , namely, $EU[s',a,d+1]$ . The act function now takes a delay argument. We interpret $C(s';d+1)$ as “the softmax action the agent would take in state $s'$ given that their rewards occur with a delay $d+1$ ”.

The Naive agent simulates his future actions by computing $C(s';d+1)$ ; the Sophisticated agent computes the action that will actually occur, which is $C(s';0)$ . So if we want to simulate an environment including a hyperbolic discounter, we can compute the agent’s action with $C(s;0)$ for every state $s$ .

Implementing the hyperbolic discounter

As with the MDP and POMDP agents, our WebPPL implementation directly translates the mathematical formulation of Naive and Sophisticated hyperbolic discounting. The variable names correspond as follows:

The function $\delta$ is named discountFunction
The “perceived delay”, which controls how the agent’s simulated future self evaluates rewards, is $d$ in the math and perceivedDelay below.
$s'$ , $a'$ , $d+1$ correspond to nextState, nextAction and delay+1 respectively.

This codebox simplifies the code for the hyperbolic discounter by omitting definitions of transition, utility and so on:

var makeAgent = function(params, world) {

  var act = dp.cache( 
    function(state, delay){
      return Infer({ model() {
        var action = uniformDraw(stateToActions(state));
        var eu = expectedUtility(state, action, delay);    
        factor(params.alpha * eu);
        return action;
      }});      
    });
  
  var expectedUtility = dp.cache(
    function(state, action, delay){
      var u = discountFunction(delay) * utility(state, action);
      if (state.terminateAfterAction){
        return u; 
      } else {                     
        return u + expectation(Infer({ model() {
          var nextState = transition(state, action); 
          var perceivedDelay = isNaive ? delay + 1 : 0;
          var nextAction = sample(act(nextState, perceivedDelay));
          return expectedUtility(nextState, nextAction, delay+1);  
        }}));
      }                      
    });
  
  return { params, expectedUtility, act };
};

The next codebox shows how the Naive agent can end up at Donut North in the Restaurant Choice problem, despite this being dominated for any possible utility function. The Naive agent first moves in the direction of Veg, which initially looks better than Donut South. When right outside Donut North, discounting makes it look better than Veg. To visualize this, we display the agent’s expected utility calculations at different steps along its trajectory. The crucial values are the expectedValue of going left at [3,5] when delay=0 compared with delay=4. The function plannedTrajectories uses expectedValue to access these values. For each timestep, we plot the agent’s position and the expected utility of each action they might perform in the future.

///fold: makeAgent, mdp, plannedTrajectories
var makeAgent = function(params, world) {
  var defaultParams = {
    alpha: 500, 
    discount: 1
  };
  var params = extend(defaultParams, params);
  var stateToActions = world.stateToActions;
  var transition = world.transition;
  var utility = params.utility;
  var paramsDiscountFunction = params.discountFunction;

  var discountFunction = (
    paramsDiscountFunction ? 
    paramsDiscountFunction : 
    function(delay){ return 1/(1 + params.discount*delay); });

  var isNaive = params.sophisticatedOrNaive === 'naive';

  var act = dp.cache( 
    function(state, delay) {
      var delay = delay || 0; // make sure delay is never undefined
      return Infer({ model() {
        var action = uniformDraw(stateToActions(state));
        var eu = expectedUtility(state, action, delay);
        factor(params.alpha * eu);
        return action;
      }});
    });

  var expectedUtility = dp.cache(
    function(state, action, delay) {
      var u = discountFunction(delay) * utility(state, action);
      if (state.terminateAfterAction){
        return u; 
      } else {
        return u + expectation(Infer({ model() {
          var nextState = transition(state, action); 
          var perceivedDelay = isNaive ? delay + 1 : 0;
          var nextAction = sample(act(nextState, perceivedDelay));
          return expectedUtility(nextState, nextAction, delay+1);
        }}));
      }
    });

  return { params, expectedUtility, act };
};

var ___ = ' '; 
var DN = { name : 'Donut N' };
var DS = { name : 'Donut S' };
var V = { name : 'Veg' };
var N = { name : 'Noodle' };

var grid = [
  ['#', '#', '#', '#',  V , '#'],
  ['#', '#', '#', ___, ___, ___],
  ['#', '#', DN , ___, '#', ___],
  ['#', '#', '#', ___, '#', ___],
  ['#', '#', '#', ___, ___, ___],
  ['#', '#', '#', ___, '#',  N ],
  [___, ___, ___, ___, '#', '#'],
  [DS , '#', '#', ___, '#', '#']
];

var mdp = makeGridWorldMDP({
  grid,
  noReverse: true,
  maxTimeAtRestaurant: 2,
  start: [3, 1],
  totalTime: 11
});

var MAPActionPath = function(state, world, agent, actualTotalTime, statesOrActions) { 
  var perceivedTotalTime = state.timeLeft;
  assert.ok(perceivedTotalTime  > 1 || state.terminateAfterAction==false,
            'perceivedTime<=1. If=1 then should have state.terminateAfterAction,' +
            ' but then simulate wont work ' + JSON.stringify(state));

  var agentAction = agent.act;
  var expectedUtility = agent.expectedUtility;
  var transition = world.transition;

  var sampleSequence = function (state, actualTimeLeft) {
    var action = agentAction(state, actualTotalTime-actualTimeLeft).MAP().val;
    var nextState = transition(state, action); 
    var out = {states:state, actions:action, both:[state,action]}[statesOrActions];
    if (actualTimeLeft==0 || state.terminateAfterAction){
      return [out];
    } else {
      return [ out ].concat( sampleSequence(nextState, actualTimeLeft-1));
    }
  };
  return sampleSequence(state, actualTotalTime);
};

var plannedTrajectory = function(world, agent) {
  var getExpectedUtilities = function(trajectory, agent, actions) { 
    var expectedUtility = agent.expectedUtility;
    var v = mapIndexed(function(i, state) {
      return [state, map(function (a) { return  expectedUtility(state, a, i); }, actions)];
    }, trajectory );
    return v;
  };
  return function(state) {
    var currentPlan = MAPActionPath(state, world, agent, state.timeLeft, 'states');
    return getExpectedUtilities(currentPlan, agent, world.actions);
  };
} 

var plannedTrajectories = function(trajectory, world, agent) { 
  var getTrajectory = plannedTrajectory(world, agent);
  return map(getTrajectory, trajectory);
}
///

var world = mdp.world;
var start = mdp.startState;

var utilityTable = {
  'Donut N': [10, -10],  // [immediate reward, delayed reward]
  'Donut S': [10, -10],
  'Veg': [-10, 20],
  'Noodle': [0, 0],
  'timeCost': -.01  // cost of taking a single action 
};

var restaurantUtility = function(state, action) {
  var feature = world.feature;
  var name = feature(state).name;
  if (name) {
    return utilityTable[name][state.timeAtRestaurant]
  } else {
    return utilityTable.timeCost;
  }
};

var runAndGraph = function(agent) { 
  var trajectory = simulateMDP(mdp.startState, world, agent);
  var plans = plannedTrajectories(trajectory, world, agent);
  viz.gridworld(world, {
    trajectory, 
    dynamicActionExpectedUtilities: plans
  });
};

var agent = makeAgent({
  sophisticatedOrNaive: 'naive', 
  utility: restaurantUtility
}, world);

print('Naive agent: \n\n');
runAndGraph(agent);

We run the Sophisticated agent with the same parameters and visualization.

///fold: 
var makeAgent = function(params, world) {
  var defaultParams = {
    alpha: 500, 
    discount: 1
  };
  var params = extend(defaultParams, params);
  var stateToActions = world.stateToActions;
  var transition = world.transition;
  var utility = params.utility;
  var paramsDiscountFunction = params.discountFunction;

  var discountFunction = (
    paramsDiscountFunction ? 
    paramsDiscountFunction : 
    function(delay){ return 1/(1+params.discount*delay); });

  var isNaive = params.sophisticatedOrNaive === 'naive';

  var act = dp.cache( 
    function(state, delay) {
      var delay = delay || 0; // make sure delay is never undefined
      return Infer({ model() {
        var action = uniformDraw(stateToActions(state));
        var eu = expectedUtility(state, action, delay);
        factor(params.alpha * eu);
        return action;
      }});
    });

  var expectedUtility = dp.cache(
    function(state, action, delay) {
      var u = discountFunction(delay) * utility(state, action);
      if (state.terminateAfterAction){
        return u; 
      } else {
        return u + expectation(Infer({ model() {
          var nextState = transition(state, action); 
          var perceivedDelay = isNaive ? delay + 1 : 0;
          var nextAction = sample(act(nextState, perceivedDelay));
          return expectedUtility(nextState, nextAction, delay+1);
        }}));
      }
    });

  return { params, expectedUtility, act };
};

var ___ = ' '; 
var DN = { name : 'Donut N' };
var DS = { name : 'Donut S' };
var V = { name : 'Veg' };
var N = { name : 'Noodle' };

var grid = [
  ['#', '#', '#', '#',  V , '#'],
  ['#', '#', '#', ___, ___, ___],
  ['#', '#', DN , ___, '#', ___],
  ['#', '#', '#', ___, '#', ___],
  ['#', '#', '#', ___, ___, ___],
  ['#', '#', '#', ___, '#',  N ],
  [___, ___, ___, ___, '#', '#'],
  [DS , '#', '#', ___, '#', '#']
];

var mdp = makeGridWorldMDP({
  grid,
  noReverse: true,
  maxTimeAtRestaurant: 2,
  start: [3, 1],
  totalTime: 11
});

var world = mdp.world;

var utilityTable = {
  'Donut N': [10, -10],  // [immediate reward, delayed reward]
  'Donut S': [10, -10],
  'Veg': [-10, 20],
  'Noodle': [0, 0],
  'timeCost': -.01  // cost of taking a single action 
};

var restaurantUtility = function(state, action) {
  var feature = world.feature;
  var name = feature(state).name;
  if (name) {
    return utilityTable[name][state.timeAtRestaurant]
  } else {
    return utilityTable.timeCost;
  }
};

var MAPActionPath = function(state, world, agent, actualTotalTime, statesOrActions) { 
  var perceivedTotalTime = state.timeLeft;
  assert.ok(perceivedTotalTime  > 1 || state.terminateAfterAction==false,
            'perceivedTime<=1. If=1 then should have state.terminateAfterAction,' +
            ' but then simulate wont work ' + JSON.stringify(state));

  var agentAction = agent.act;
  var expectedUtility = agent.expectedUtility;
  var transition = world.transition;

  var sampleSequence = function (state, actualTimeLeft) {
    var action = agentAction(state, actualTotalTime-actualTimeLeft).MAP().val;
    var nextState = transition(state, action); 
    var out = {states:state, actions:action, both:[state,action]}[statesOrActions];
    if (actualTimeLeft==0 || state.terminateAfterAction){
      return [out];
    } else {
      return [ out ].concat( sampleSequence(nextState, actualTimeLeft-1));
    }
  };
  return sampleSequence(state, actualTotalTime);
};

var plannedTrajectory = function(world, agent) {
  var getExpectedUtilities = function(trajectory, agent, actions) { 
    var expectedUtility = agent.expectedUtility;
    var v = mapIndexed(function(i, state) {
      return [state, map(function (a) { return  expectedUtility(state, a, i); }, actions)];
    }, trajectory );
    return v;
  };
  return function(state) {
    var currentPlan = MAPActionPath(state, world, agent, state.timeLeft, 'states');
    return getExpectedUtilities(currentPlan, agent, world.actions);
  };
};

var plannedTrajectories = function(trajectory, world, agent) { 
  var getTrajectory = plannedTrajectory(world, agent);
  return map(getTrajectory, trajectory);
};

var runAndGraph = function(agent) { 
  var trajectory = simulateMDP(mdp.startState, world, agent);
  var plans = plannedTrajectories(trajectory, world, agent);
  viz.gridworld(world, {
    trajectory, 
    dynamicActionExpectedUtilities: plans
  });
};
///

var agent = makeAgent({
  sophisticatedOrNaive: 'sophisticated', 
  utility: restaurantUtility
}, world);

print('Sophisticated agent: \n\n');
runAndGraph(agent);

Exercise: What would an exponential discounter with identical preferences to the agents above do on the Restaurant Choice problem? Implement an exponential discounter in the codebox above by adding a discountFunction property to the params argument to makeAgent.

Example: Procrastinating on a task

Compared to the Restaurant Choice problem, procrastination leads to (systematically biased) behavior that is especially hard to explain on the softmax noise mode.

The Procrastination Problem
You have a hard deadline of ten days to complete a task (e.g. write a paper for class, apply for a school or job). Completing the task takes a full day and has a cost (it’s unpleasant work). After the task is complete you get a reward (typically exceeding the cost). There is an incentive to finish early: every day you delay finishing, your reward gets slightly smaller. (Imagine that it’s good for your reputation to complete tasks early or that early applicants are considered first).

Note that if the task is worth doing at the last minute, then you should do it immediately (because the reward diminishes over time). Yet people often do this kind of task at the last minute – the worst possible time to do it!

Hyperbolic discounting provides an elegant model of this behavior. On Day 1, a hyperbolic discounter will prefer that they complete the task tomorrow rather than today. Moreover, a Naive agent wrongly predicts they will complete the task tomorrow and so puts off the task till Day 2. When Day 2 arrives, the Naive agent reasons in the same way – telling themself that they can avoid the work today by putting it off till tomorrow. This continues until the last possible day, when the Naive agent finally completes the task.

In this problem, the behavior of optimal and time-inconsistent agents with identical preferences (i.e. utility functions) diverges. If the deadline is $T$ days from the start, the optimal agent will do the task immediately and the Naive agent will do the task on Day $T$ . Any problem where a time-inconsistent agent receives exponentially lower reward than an optimal agent contains a close variant of our Procrastination Problem refp:kleinberg2014time ¹.

We formalize the Procrastination Problem in terms of a deterministic graph. Suppose the deadline is $T$ steps from the start. Assume that after $t$ < $T$ steps the agent has not yet completed the task. Then the agent can take the action "work" (which has work cost $-w$ ) or the action "wait" with zero cost. After the "work" action the agent transitions to the "reward" state and receives $+(R - t \epsilon)$ , where $R$ is the reward for the task and $\epsilon$ is how much the reward diminishes for every day of waiting (the wait cost). See Figure 3 below.

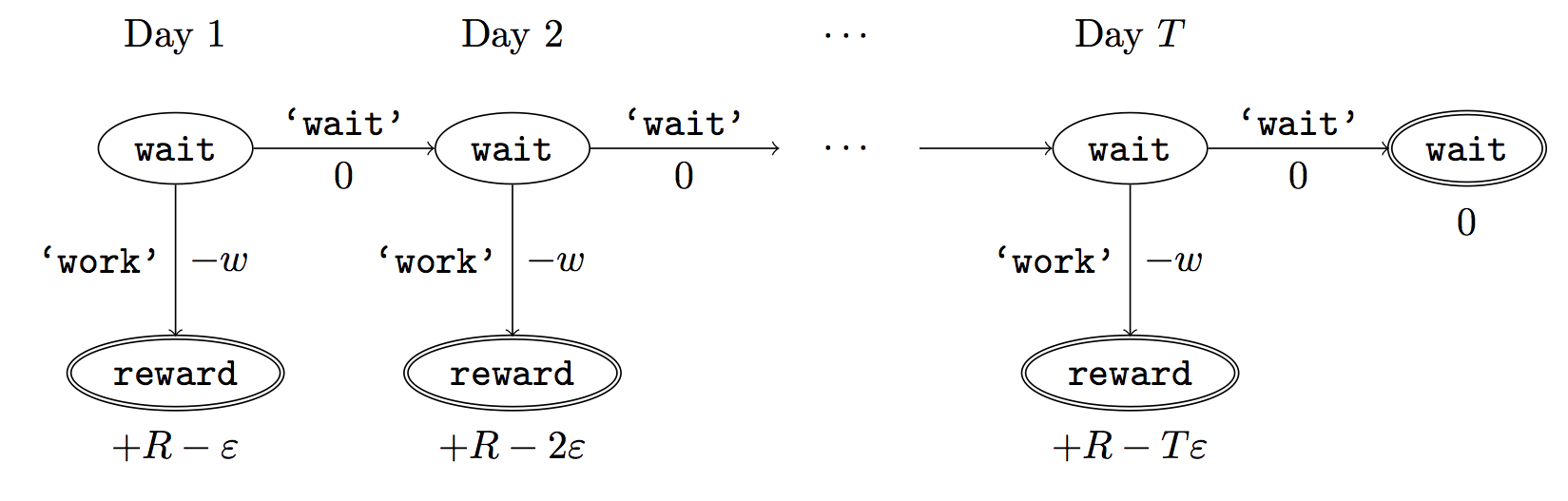
diagram

Figure 3: Transition graph for Procrastination Problem. States are represented by nodes. Edges are state-transitions and are labeled with the action name and the utility of the state-action pair. Terminal nodes have a bold border and their utility is labeled below.

We simulate the behavior of hyperbolic discounters on the Procrastination Problem. We vary the discount rate $k$ while holding the other parameters fixed. The agent’s behavior can be summarized by its final state ("wait_state" or "reward_state) and by how much time elapses before termination. When $k$ is sufficiently high, the agent will not even complete the task on the last day.

///fold: makeProcrastinationMDP, makeProcrastinationUtility
var makeProcrastinationMDP = function(deadlineTime) {
  var stateLocs = ["wait_state", "reward_state"];
  var actions = ["wait", "work", "relax"];

  var stateToActions = function(state) {
    return (state.loc === "wait_state" ? 
            ["wait", "work"] :
            ["relax"]);
  };

  var advanceTime = function (state) {
    var newTimeLeft = state.timeLeft - 1;
    var terminateAfterAction = (newTimeLeft === 1 || 
                                state.loc === "reward_state");
    return extend(state, {
      timeLeft: newTimeLeft,
      terminateAfterAction: terminateAfterAction
    });
  };

  var transition = function(state, action) {
    assert.ok(_.includes(stateLocs, state.loc) && _.includes(actions, action), 
              'procrastinate transition:' + [state.loc,action]);
    
    if (state.loc === "reward_state") {
      return advanceTime(state);
    } else if (action === "wait") {
      var waitSteps = state.waitSteps + 1;
      return extend(advanceTime(state), { waitSteps });
    } else {
      var newState = extend(state, { loc: "reward_state" });
      return advanceTime(newState);
    }
  };

  var feature = function(state) {
    return state.loc;
  };

  var startState = {
    loc: "wait_state",
    waitSteps: 0,
    timeLeft: deadlineTime,
    terminateAfterAction: false
  };

  return {
    actions,
    stateToActions,
    transition,
    feature,
    startState
  };
};


var makeProcrastinationUtility = function(utilityTable) {
  assert.ok(hasProperties(utilityTable, ['waitCost', 'workCost', 'reward']),
            'makeProcrastinationUtility args');
  var waitCost = utilityTable.waitCost;
  var workCost = utilityTable.workCost;
  var reward = utilityTable.reward;

  // NB: you receive the *workCost* when you leave the *wait_state*
  // You then receive the reward when leaving the *reward_state* state
  return function(state, action) {
    if (state.loc === "reward_state") {
      return reward + state.waitSteps * waitCost;
    } else if (action === "work") {
      return workCost;
    } else {
      return 0;
    }
  };
};
///

// Construct Procrastinate world 
var deadline = 10;
var world = makeProcrastinationMDP(deadline);

// Agent params
var utilityTable = {
  reward: 4.5,
  waitCost: -0.1,
  workCost: -1
};

var params = {
  utility: makeProcrastinationUtility(utilityTable),
  alpha: 1000,
  discount: null,
  sophisticatedOrNaive: 'sophisticated'
};

var getLastState = function(discount){
  var agent = makeMDPAgent(extend(params, { discount: discount }), world);
  var states = simulateMDP(world.startState, world, agent, 'states');
  return [last(states).loc, states.length];
};

map(function(discount) {
  var lastState = getLastState(discount);
  print('Discount: ' + discount + '. Last state: ' + lastState[0] +
        '. Time: ' + lastState[1] + '\n')
}, _.range(8));

Exercise:

Explain how an exponential discounter would behave on this task. Assume their utilities are the same as above and consider different discount rates.

Run the codebox above with a Sophisticated agent. Explain the results.

Next chapter: Myopia for rewards and belief updates

Footnotes

Kleinberg and Oren’s paper considers a variant problem where the each cost/penalty for waiting is received immediately (rather than being delayed until the time the task is done). In this variant, the agent must eventually complete the task. The authors consider “semi-myopic” time-inconsistent agents, i.e. agents who do not discount their next reward, but discount all future rewards by $\beta < 1$ . They show that in any problem where a semi-myopic agent receives exponentially lower reward than an optimal agent, the problem must contain a copy of their variant of the Procrastination Problem. ↩