Joint inference of biases and preferences I

Introduction

Techniques for inferring human preferences and beliefs from their behavior on a task usually assume that humans solve the task (softmax) optimally. When this assumptions fails, inference often fails too. This chapter explores how incorporating time inconsistency and myopic planning into models of human behavior can improve inference.

Formalization of Joint Inference

We formalize joint inference over beliefs, preferences and biases by extending the approach developed in Chapter IV, “Reasoning about Agents”, where an agent was formally defined by parameters $\left\langle U, \alpha, b_0 \right\rangle$ . To include the possibility of time-inconsistency and myopia, an agent $\theta$ is now characterized by a tuple of parameters as follows:

$\theta = \left\langle U, \alpha, b_0, k, \nu, C \right\rangle$

where:

$U$ is the utilty function
$\alpha$ is the softmax noise parameter
$b_0$ is the agent’s belief (or prior) over the initial state
$k \geq 0$ is the constant for hyperbolic discounting function $1/(1+kd)$
$\nu$ is an indicator for Naive or Sophisticated hyperbolic discounting
$C \in [1,\infty]$ is the integer cutoff or bound for Reward-myopic or Update-myopic Agents¹

As in Equation (2) of Chapter IV, we condition on state-action-observation triples:

$P(\theta \vert (s,o,a)_{0:n}) \propto P( (s,o,a)_{0:n} \vert \theta)P(\theta)$

We obtain a factorized form in exactly the same way as in Equation (2), i.e. we generate the sequence $b_i$ from $i=0$ to $i=n$ of agent beliefs:

$P(\theta \vert (s,o,a)_{0:n}) \propto P(\theta) \prod_{i=0}^n P( a_i \vert s_i, b_i, U, \alpha, k, \nu, C )$

The likelihood term on the right-hand side of this equation is simply the softmax probability that the agent with given parameters chooses $a_i$ in state $s_i$ . This equation for inference does not make use of the delay indices used by time-inconsistent and Myopic agents. This is because the delays figure only in their internal simulations. In order to compute the likelihood the agent takes an action, we don’t need to keep track of delay values.

Learning from Procrastinators

The Procrastination Problem (Figure 1 below) illustrates how agents with identical preferences can deviate systematically in their behavior due to time inconsistency. Suppose two agents care equally about finishing the task and assign the same cost to doing the hard work. The optimal agent will complete the task immediately. The Naive hyperbolic discounter will delay every day until the deadline, which could be thirty days away!

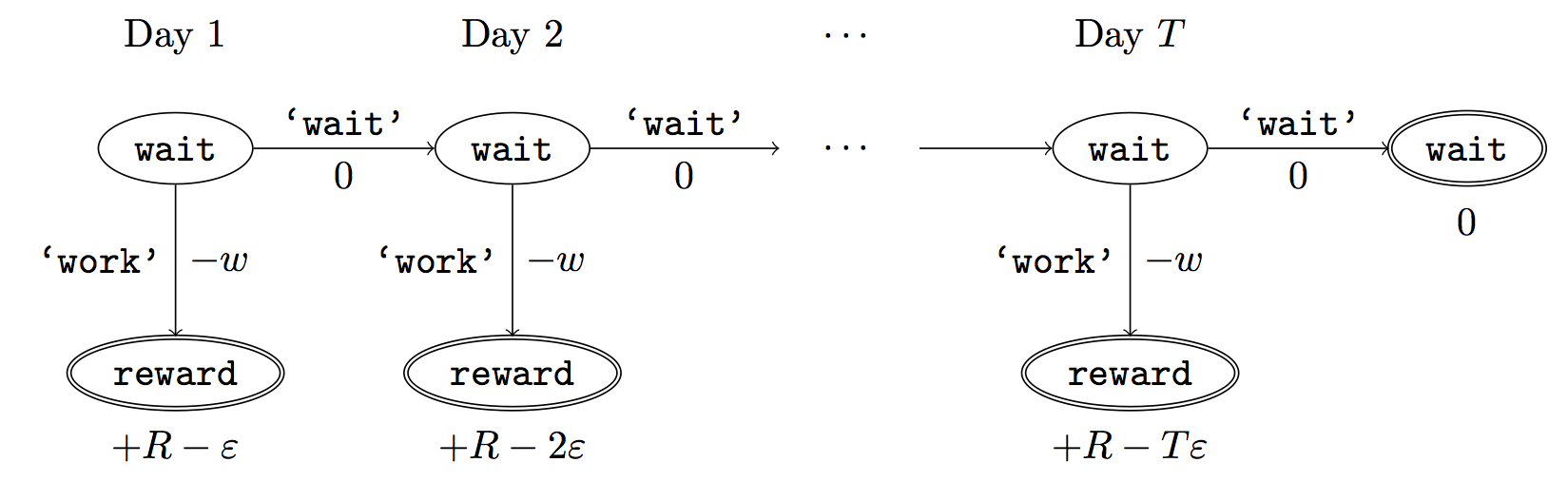
diagram

Figure 1: Transition graph for Procrastination Problem. States are represented by nodes. Edges are state-transitions and are labeled with the action name and the utility of the state-action pair. Terminal nodes have a bold border and their utility is labeled below.

This kind of systematic deviation between agents is also significant for inferring preferences. We consider the problem of online inference, where we observe the agent’s behavior each day and produce an estimate of their preferences. Suppose the agent has a deadline $T$ days into the future and leaves the work till the last day. This is typical human behavior – and so is a good test for a model of inference.

We compare the online inferences of two models. The Optimal Model assumes the agent is time-consistent with softmax parameter $\alpha$ . The Possibly Discounting model includes both optimal and Naive hyperbolic discounting agents in its prior. (The Possibly Discounting model includes the Optimal Model as a special case; this allows us to place a uniform prior on the models and exploit Bayesian Model Selection.)

For each model, we compute posteriors for the agent’s parameters after observing the agent’s choice at each timestep. We set $T=10$ . So the observed actions are:

["wait", "wait", "wait", ... , "work"]

where "work" is the final action. We fix the utilities for doing the work (the workCost or $-w$ ) and for delaying the work (the waitCost or $-\epsilon$ ). We infer the following parameters:

The reward received after completing the work: $R$ or reward
The agent’s softmax parameter: $\alpha$
The agent’s discount rate (for the Possibly Discounting model): $k$ or discount

Note that we are not just inferring whether the agent is biased; we also infer how biased they are. For each parameter, we plot a time-series showing the posterior expectation of the parameter on each day. We also plot the model’s posterior predictive probability that the agent does the work on the last day (assuming the agent gets to the last day without having done the work).

// infer_procrastination

///fold: makeProcrastinationMDP, makeProcrastinationUtility, displayTimeSeries, ...
var makeProcrastinationMDP = function(deadlineTime) {
  var stateLocs = ["wait_state", "reward_state"];
  var actions = ["wait", "work", "relax"];

  var stateToActions = function(state) {
    return (state.loc === "wait_state" ? 
            ["wait", "work"] :
            ["relax"]);
  };

  var advanceTime = function (state) {
    var newTimeLeft = state.timeLeft - 1;
    var terminateAfterAction = (newTimeLeft === 1 || 
                                state.loc === "reward_state");
    return extend(state, {
      timeLeft: newTimeLeft,
      terminateAfterAction: terminateAfterAction
    });
  };

  var transition = function(state, action) {
    assert.ok(_.includes(stateLocs, state.loc) && _.includes(actions, action), 
              'procrastinate transition:' + [state.loc,action]);
    
    if (state.loc === "reward_state") {
      return advanceTime(state);
    } else if (action === "wait") {
      var waitSteps = state.waitSteps + 1;
      return extend(advanceTime(state), { waitSteps });
    } else {
      var newState = extend(state, { loc: "reward_state" });
      return advanceTime(newState);
    }
  };

  var feature = function(state) {
    return state.loc;
  };

  var startState = {
    loc: "wait_state",
    waitSteps: 0,
    timeLeft: deadlineTime,
    terminateAfterAction: false
  };

  return {
    actions,
    stateToActions,
    transition,
    feature,
    startState
  };
};

var makeProcrastinationUtility = function(utilityTable) {
  assert.ok(hasProperties(utilityTable, ['waitCost', 'workCost', 'reward']),
            'makeProcrastinationUtility args');
  var waitCost = utilityTable.waitCost;
  var workCost = utilityTable.workCost;
  var reward = utilityTable.reward;

  // NB: you receive the *workCost* when you leave the *wait_state*
  // You then receive the reward when leaving the *reward_state* state
  return function(state, action) {
    if (state.loc === "reward_state") {
      return reward + state.waitSteps * waitCost;
    } else if (action === "work") {
      return workCost;
    } else {
      return 0;
    }
  };
};

var getMarginal = function(dist, key){
  return Infer({ model() {
    return sample(dist)[key];
  }});
};

var displayTimeSeries = function(observedStateAction, getPosterior) {
  var features = ['reward', 'predictWorkLastMinute', 'alpha', 'discount'];

  // dist on {a:1, b:3, ...} -> [E('a'), E('b') ... ]
  var distToMarginalExpectations = function(dist, keys) {
    return map(function(key) {
      return expectation(getMarginal(dist, key));
    }, keys);
  };
  // condition observations up to *timeIndex* and take expectations
  var inferUpToTimeIndex = function(timeIndex, useOptimalModel) {
    var observations = observedStateAction.slice(0, timeIndex);
    return distToMarginalExpectations(getPosterior(observations, useOptimalModel), features);
  };

  var getTimeSeries = function(useOptimalModel) {

    var inferAllTimeIndexes = map(function(index) {
      return inferUpToTimeIndex(index, useOptimalModel);
    }, _.range(observedStateAction.length));

    return map(function(i) {
      // get full time series of online inferences for each feature
      return map(function(infer){return infer[i];}, inferAllTimeIndexes);
    }, _.range(features.length));
  };

  var displayOptimalAndPossiblyDiscountingSeries = function(index) {
    print('\n\nfeature: ' + features[index]);
    var optimalSeries = getTimeSeries(true)[index];
    var possiblyDiscountingSeries = getTimeSeries(false)[index];
    var plotOptimal = map(
      function(pair){ 
        return {
          t: pair[0], 
          expectation: pair[1], 
          agentModel: 'Optimal'
        };
      },
      zip(_.range(observedStateAction.length), optimalSeries));
    var plotPossiblyDiscounting = map(
      function(pair){
        return {
          t: pair[0],
          expectation: pair[1],
          agentModel: 'Possibly Discounting'
        };
      },
      zip(_.range(observedStateAction.length),
          possiblyDiscountingSeries));
    viz.line(plotOptimal.concat(plotPossiblyDiscounting), 
             { groupBy: 'agentModel' });
  };

  print('Posterior expectation on feature after observing ' +
        '"wait" for t timesteps and "work" when t=9');
  map(displayOptimalAndPossiblyDiscountingSeries, _.range(features.length));
  return '';
};

var procrastinationData = [[{"loc":"wait_state","waitSteps":0,"timeLeft":10,"terminateAfterAction":false},"wait"],[{"loc":"wait_state","waitSteps":1,"timeLeft":9,"terminateAfterAction":false},"wait"],[{"loc":"wait_state","waitSteps":2,"timeLeft":8,"terminateAfterAction":false},"wait"],[{"loc":"wait_state","waitSteps":3,"timeLeft":7,"terminateAfterAction":false},"wait"],[{"loc":"wait_state","waitSteps":4,"timeLeft":6,"terminateAfterAction":false},"wait"],[{"loc":"wait_state","waitSteps":5,"timeLeft":5,"terminateAfterAction":false},"wait"],[{"loc":"wait_state","waitSteps":6,"timeLeft":4,"terminateAfterAction":false},"wait"],[{"loc":"wait_state","waitSteps":7,"timeLeft":3,"terminateAfterAction":false},"wait"],[{"loc":"wait_state","waitSteps":8,"timeLeft":2,"terminateAfterAction":false},"work"],[{"loc":"reward_state","waitSteps":8,"timeLeft":1,"terminateAfterAction":true},"relax"]];
///

var getPosterior = function(observedStateAction, useOptimalModel) {
  var world = makeProcrastinationMDP();
  var lastChanceState = secondLast(procrastinationData)[0];

  return Infer({ model() {

    var utilityTable = {
      reward: uniformDraw([0.5, 2, 3, 4, 5, 6, 7, 8]),
      waitCost: -0.1,
      workCost: -1
    };
    var params = {
      utility: makeProcrastinationUtility(utilityTable),
      alpha: categorical([0.1, 0.2, 0.2, 0.2, 0.3], [0.1, 1, 10, 100, 1000]),
      discount: useOptimalModel ? 0 : uniformDraw([0, .5, 1, 2, 4]),
      sophisticatedOrNaive: 'naive'
    };

    var agent = makeMDPAgent(params, world);
    var act = agent.act;

    map(function(stateAction) {
      var state = stateAction[0];
      var action = stateAction[1];
      observe(act(state, 0), action);
    }, observedStateAction);

    return {
      reward: utilityTable.reward, 
      alpha: params.alpha, 
      discount: params.discount, 
      predictWorkLastMinute: sample(act(lastChanceState, 0)) === 'work'
    };
  }});
};

displayTimeSeries(procrastinationData, getPosterior);

The optimal model makes inferences that clash with everyday intuition. Suppose someone has still not done a task with only two days left. Would you confidently rule out them doing it at the last minute?

With two days left, the Optimal model has almost complete confidence that the agent doesn’t care about the task enough to do the work (reward < workCost = 1). Hence it assigns probability $0.005$ to the agent doing the task at the last minute (predictWorkLastMinute). By contrast, the Possibly Discounting model predicts the agent will do the task with probability around $0.2$ . The predictive probability is no higher than $0.2$ because the Possibly Discounting model allows the agent to be optimal (discount==0) and because a sub-optimal agent might be too lazy to do the work even at the last minute (i.e. discount is high enough to overwhelm reward).

Suppose someone completes the task on the final day. What do you infer about them? The Optimal Model has to explain the action by massively revising its inference about reward and $\alpha$ . It suddenly infers that the agent is extremely noisy and that reward > workCost by a big margin. The extreme noise is needed to explain why the agent would miss a good option nine out of ten times. By contrast, the Possibly Discounting Model does not change its inference about the agent’s noise level very much at all (in terms of pratical significance). It infers a much higher value for reward, which is plausible in this context.

Learning from Reward-myopic Agents in Bandits

Chapter V.2. “Bounded Agents” explained that Reward-myopic agents explore less than optimal agents. The Reward-myopic agent plans each action as if time runs out in $C_g$ steps, where $C_g$ is the bound or “look ahead”. If exploration only pays off in the long-run (after the bound) then the agent won’t explore². This means there are two possible explanations for an agent not exploring: either the agent is greedy or the agent has a low prior on the utility of the unknown options.

We return to the deterministic bandit-style problem from earlier. At each trial, the agent chooses between two arms with the following properties:

arm0: yields chocolate
arm1: yields either champagne or no prize at all (agent’s prior is $0.7$ for nothing)

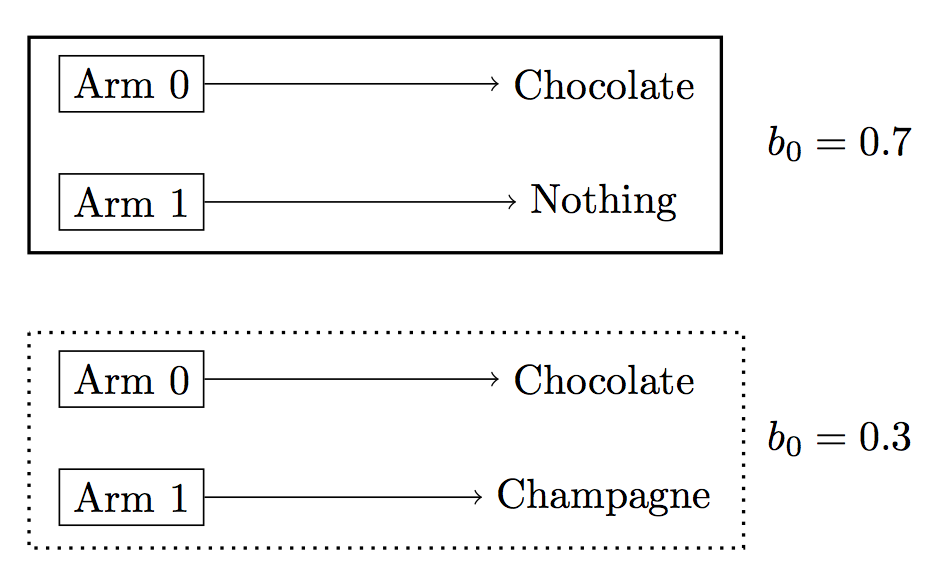
diagram

The inference problem is to infer the agent’s preference over chocolate. While having only two deterministic arms may seem overly simple, the same structure is shared by realistic problems. For example, we can imagine observing people choosing between different cuisines, restaurants or menu options. Usually people know about some options well but are uncertain about others. When inferring their preferences, we distinguish between options chosen for exploration vs. exploitation. The same applies to people choosing media sources: someone might try out a channel to learn whether it shows their favorite genre.

As with the Procrastination example above, we compare the inferences of two models. The Optimal Model assumes the agent solves the POMDP optimally. The Possibly Reward-myopic Model includes both the optimal agent and Reward-myopic agents with different values for the bound $C_g$ . The models know the agent’s utility for champagne and his prior about how likely champagne is from arm1. The models have a fixed prior on the agent’s utility for chocolate. We vary the agent’s time horizon between 2 and 10 timesteps and plot posterior expectations for the utility of chocolate. For the Possibly Reward-myopic model, we also plot the expectation for $C_g$ .

// helper function to assemble and display inferred values
///fold:
var timeHorizonValues = _.range(10).slice(2);
var features = ['Utility of arm 0 (chocolate)', 'Greediness bound'];

var displayExpectations = function(getPosterior) {

  var getExpectations = function(useOptimalModel) {

    var inferAllTimeHorizons = map(function(horizon) {
      return getPosterior(horizon, useOptimalModel);
    }, timeHorizonValues);

    return map(
      function(i) {
        return map(function(infer){return infer[i];}, inferAllTimeHorizons);
      }, 
      _.range(features.length));
  };

  var displayOptimalAndPossiblyRewardMyopicSeries = function(index) {
    print('\n\nfeature: ' + features[index]);
    var optimalSeries = getExpectations(true)[index];
    var possiblyRewardMyopicSeries = getExpectations(false)[index];
    var plotOptimal = map(
      function(pair) {
        return {
          horizon: pair[0], 
          expectation: pair[1], 
          agentModel: 'Optimal'
        };
      },
      zip(timeHorizonValues, optimalSeries));
    var plotPossiblyRewardMyopic = map(
      function(pair){
        return {
          horizon: pair[0], 
          expectation: pair[1],
          agentModel: 'Possibly RewardMyopic'
        };
      },
      zip(timeHorizonValues, possiblyRewardMyopicSeries));
    viz.line(plotOptimal.concat(plotPossiblyRewardMyopic), 
             { groupBy: 'agentModel' });
  };

  print('Posterior expectation on feature after observing no exploration');
  map(displayOptimalAndPossiblyRewardMyopicSeries, _.range(features.length));
  return '';
};

var getMarginal = function(dist, key){
  return Infer({ model() {
    return sample(dist)[key];
  }});
};
///


var getPosterior = function(numberOfTrials, useOptimalModel) {
  var trueArmToPrizeDist = {
    0: Delta({ v: 'chocolate' }),
    1: Delta({ v: 'nothing' })
  };
  var bandit = makeBanditPOMDP({
    numberOfArms: 2,
    armToPrizeDist: trueArmToPrizeDist,
    numberOfTrials: numberOfTrials
  });

  var startState = bandit.startState;
  var alternativeArmToPrizeDist = extend(trueArmToPrizeDist,
                                         { 1: Delta({ v: 'champagne' }) });
  var alternativeStartState = makeBanditStartState(numberOfTrials,
                                                   alternativeArmToPrizeDist);

  var priorAgentPrior = Delta({ 
    v: Categorical({ 
      vs: [startState, alternativeStartState],      
      ps: [0.7, 0.3]
    })
  });

  var priorPrizeToUtility = Infer({ model() {
    return {
      chocolate: uniformDraw(_.range(20).concat(25)),
      nothing: 0,
      champagne: 20
    };
  }});

  var priorMyopia =  (
    useOptimalModel ? 
    Delta({ v: { on: false, bound:0 }}) :
    Infer({ model() {
      return { 
        bound: categorical([.4, .2, .1, .1, .1, .1], 
                           [1, 2, 3, 4, 6, 10]) 
      };
    }}));

  var prior = { priorAgentPrior, priorPrizeToUtility, priorMyopia };

  var baseAgentParams = {
    alpha: 1000,
    sophisticatedOrNaive: 'naive',
    discount: 0,
    noDelays: useOptimalModel
  };
  
  var observations = [[startState, 0]];

  var outputDist = inferBandit(bandit, baseAgentParams, prior, observations,
                               'offPolicy', 0, 'beliefDelay');

  var marginalChocolate = Infer({ model() {
    return sample(outputDist).prizeToUtility.chocolate;
  }});

  return [
    expectation(marginalChocolate), 
    expectation(getMarginal(outputDist, 'myopiaBound'))
  ];
};

print('Prior expected utility for arm0 (chocolate): ' + 
      listMean(_.range(20).concat(25)) );

displayExpectations(getPosterior);

The graphs show that as the agent’s time horizon increases the inferences of the two models diverge. For the Optimal agent, the longer time horizon makes exploration more valuable. So the Optimal model infers a higher utility for the known option as the time horizon increases. By contrast, the Possibly Reward-myopic model can explain away the lack of exploration by the agent being Reward-myopic. This latter model infers slightly lower values for $C_g$ as the horizon increases.

Exercise: Suppose that instead of allowing the agent to be greedy, we allowed the agent to be a hyperbolic discounter. Think about how this would affect inferences from the observations above and for other sequences of observation. Change the code above to test out your predictions.

Next chapter: Joint inference of biases and preferences II

Footnotes

To simplify the presentation, we assume here that one does inference either about whether the agent is Update-myopic or about whether the agent is Reward-myopic (but not both). It’s actually straightforward to include both kinds of agents in the hypothesis space and infer both $C_m$ and $C_g$ . ↩
If there’s no noise in transitions or in selection of actions, the Reward-myopic agent will never explore and will do poorly. ↩